Archimedean polyhedra
Here are templates for making paper models for each of the 5 Platonic solids and the 13 Archimedean semi-regular polyhedra. You are free to use them for any non-commercial purpose, as long as the copyright notice on each page is retained.
Here's a complete set of the Archimedean polyhedra:
I think that they are pretty straightforward to assemble without any instructions — just cut them out carefully, fold along the black lines, and tape. In some cases you'll need to print multiple copies of a template. The parenthesized numbers before each name tells you what each vertex should look like: in a (3,4,3,4) cuboctahedron, for instance, each vertex should be surrounded by a triangle, a square, another triangle, and other square, in order as you go around the vertex. Knowing this can be helpful when you're trying to fold the pieces up and figure out what pairs of edges match up.
For best results, print these templates out on cardstock, or print them on regular paper and use a pin to transfer the template to something heavier. Each template is fitted within the printable area of a Tektronix Phaser 360 color printer (which is what I used in making mine). If your printer has a smaller printable area, some edges may get cut off. Sorry.
All of the models have a common edge length, so relative sizes are meaningful. The squares on the smallest (the cuboctahedron) are the same size as the squares of the largest (the truncated icosidodecahedron). This means that some of the polyhedra turn out very large, and take several sheets of paper. The largest one requires seven pages of template and is roughly nine inches in diameter when completed.
Start by making the Platonic solids and the smaller Archimedeans first. The larger ones are trickier to cut out and assemble.
If you don't have it already, you'll need the free Adobe Acrobat Reader.
Platonic solids
(3,3,3) tetrahedron
(4,4,4) cube
(3,3,3,3) octahedron
(3,3,3,3,3) icosahedron
These four all fit on the same page; by printing out one copy of the page you can make them all.
|
| platonic1.pdf |
(5,5,5) dodecahedron
|
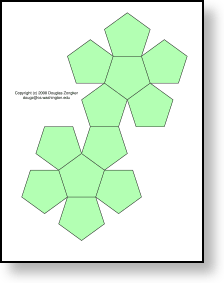
| platonic2.pdf |
Archimedean semi-regular polyhedra
(3,6,6) truncated tetrahedron
(3,4,3,4) cuboctahedron
These two fit on the same page; by printing out one copy of the page you can make them both. The cuboctahedron is the one on top.
|
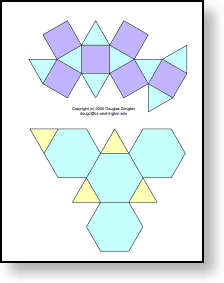
| 366-3434.pdf |
(4,6,6) truncated octahedron
This comes in two identical pieces; you need them both to make a single polyhedron.
|
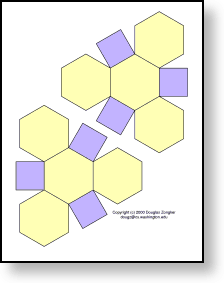
| 466.pdf |
(3,8,8) truncated cube
This comes in two identical pieces; you need them both to make a single polyhedron.
|
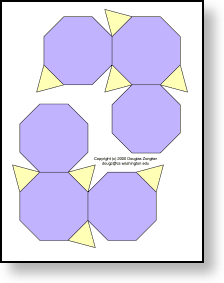
| 388.pdf |
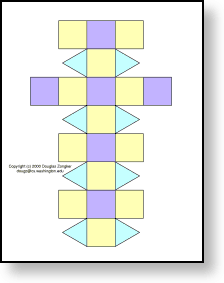
(3,4,4,4) rhombicuboctahedron
A single copy of this page will fold up into the rhombicuboctahedron.
|
| 3444.pdf |
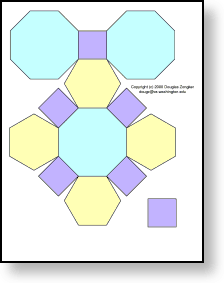
(4,6,8) truncated cuboctahedron
Print two copies of this page to get four pieces, two of which are individual squares. The bottom side of the bottom hexagon of one big piece fits up against the free side of the top square of the other piece, leaving a square hole on each side.
|
| 468.pdf |
(3,3,3,3,4) snub cuboctahedron
This shape comes from just a single piece. You can imagine creating this shape by taking the (3,4,4,4) rhombicuboctahedron and turning each yellow square into two yellow triangles. That's why there are two different colors of triangle in this model — the blue ones are the eight blue triangles already present in the rhombicuboctahedron.
|
| 33334.pdf |
(3,5,3,5) icosidodecahedron
This comes in two identical pieces; you need them both to make a single polyhedron. This is relatively easy to cut out and assemble, but the folding stage can be tricky.
|
| 3535.pdf |
(5,6,6) truncated icosahedron
Everyone's favorite polyhedron — the shape of soccerballs and buckyballs.
You need two copies of this page. Notice how each big piece consists of a central pentagon with double-hexagon "arms" radiating out, except that one of the arms has only a single hex. This is where the individual hexagon should be attached. Once this is done you'll have two star-shaped pieces that fold up into big bowls, and then the rims of the bowls can be matched up.
The most difficult part of making this one is cutting it out, because of those lightning-bolt-shaped "alleyways" that come in from the perimeter.
|
| 566.pdf |
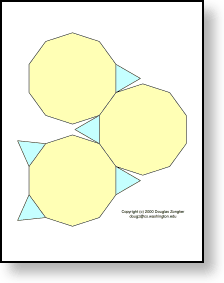
(3,10,10) truncated dodecahedron
The soccerball's evil twin. You'll need four copies of this page to put it together (decagons take a lot of room on the page!).
If you're having trouble figuring out how the pieces fit together, read the notes for the last shape, the (3,3,3,3,5) snub icosidodecahedron.
|
| 31010.pdf |
(3,4,5,4) rhombicosidodecahedron
Print out two copies to get the six total pieces you'll need. The two star shapes fold up into shallow bowls. Two copies of the snake plus the two individual squares can be strung together to make a belt around the equator that joins the bowls together — just continue the alternating triangles and squares pattern.
|
| 3454.pdf |
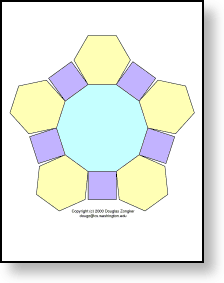
(4,6,10) truncated icosidodecahedron
The largest shape, and the only one to require two different pages. You'll need two copes of shape A on the left, which will make two very shallow bowls, or caps. Five copies of shape B, on the right, will join together in a rotationally symmetric way to make a very wide band that joins the two caps together.
|
|
| 4610a.pdf | 4610b.pdf |
(3,3,3,3,5) snub icosidodecahedron
Print two copies to make four identical pieces. This is probably the most difficult to assemble because the faces are small and the dihedral angles are large.
Each of the four pieces has threefold rotational symmetry (once it's taped up into a shallow bowl), except for a single blue triangle that sticks out in one place. This is also the case for the (3,10,10) truncated dodecahedron; the four pieces fit together in analogous ways. You should be able to fit two pieces together to make a kind of U-shape; a second identical U-shape will complete the polyhedron with a 90-degree rotation (think of how a baseball is stitched together from two pieces). Keep in mind that a blue triangle should be adjacent to three yellow triangles, and that each yellow triangle should be adjacent to exactly one blue triangle, one yellow triangle, and one purple pentagon.
|
| 33335.pdf |